用白话来说,就是为了“美,为了“好看”。

到底什么是“美”?美在哪里?先说角度。
小学初中的时候,我们三角形里只有角,最多加个直角和圆角。很明显,此时的角度只是一个很小的范围,但是实际使用中使用了很多不在这个范围内的角度,所以我们有必要对角度的概念进行扩展。这个扩展需要改变角度的定义。
角度的定义
初中(展开前):由一点出发的两条射线组成的图形。其中,两条射线称为角的两条边,端点称为角的顶点。
高中(展开后):一条射线从一个位置绕端点旋转到另一个位置形成的图形。其中:起始位置称为角度的开始边,终止位置称为角度的结束边,终点仍称为角度的顶点。

的正负角
我们规定逆时针旋转的角为正角,顺时针旋转的角为负角,不旋转的光线形成的角为零度角。
角度的分类
为了方便讨论角度,我们把角度放在直角坐标系中,即把角度的顶点放在坐标原点,把角度的起点放在轴的正方向,把角度按其终点位置对角分类:极限角度和轴上的角度。
角度表示
因为角度是放在直角坐标系中的,所以所有角度的起始边都是一样的,不同的角度只能通过角度的结束边来判断。如果两个角相等,它们角的端边一定相同;反之,不一定。
弧度
(1)引入arc系统的原因
应该说,角度概念的拓展完全可以研究函数,但在研究函数的过程中,角度体系有其不便之处:在角度中,度、分、秒都是60十进制,计算不便。更重要的是,三角函数的值是十进制的,在实际应用中会带来很多不便,尤其是对于数形结合。比如画三角函数时,因为横轴(角度和圆弧图形的使用会变得“漂亮”。
(2)电弧系统的引入:
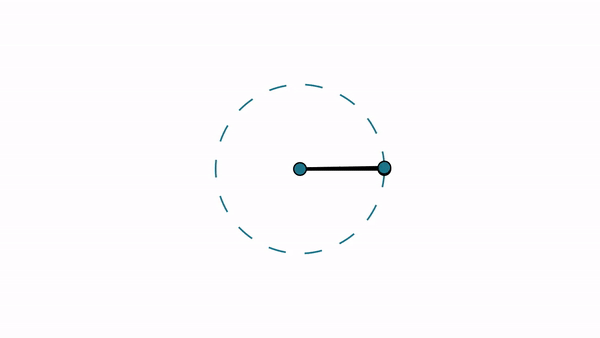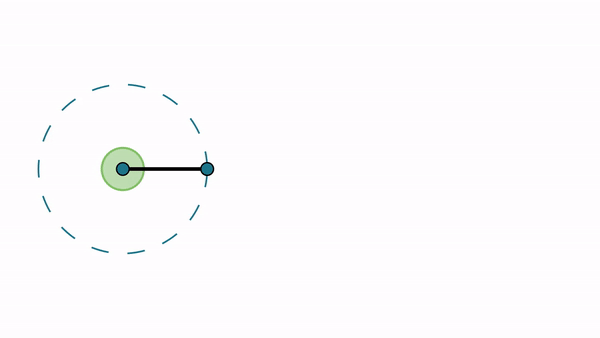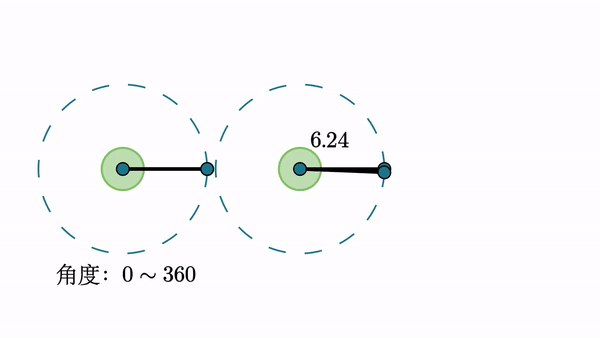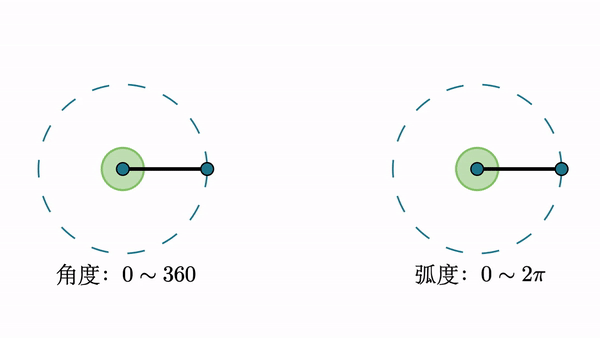
弧系是一种新的测量角度的系统,必然与弧有关,弧出现在圆里。初中解释圆时,规定圆弧的度数与圆心角的度数相同,可见角与圆弧有关。要指定新的测量系统,应首先指定单位量,对于圆弧系统,应首先指定1弧度。

1弧度角:一个圆中弧长等于半径的弧的圆心角称为1弧度角。
获得1弧度的角度后,可以用它测量其他角度。直角的弧度数等于π,圆角的弧度数等于2π。
弧系的基本思想的雏形起源于印度,但严格地说,弧的概念是在1748年由瑞士数学家莱昂哈德·欧拉(1707年4月15日-1783年9月18日)引入的。

关于弧度“弧度”的由来有一种说法:由于弧度π等于半周长与半径之比,数学家将半径的前四个字母与角度的前两个字母组合起来,组成了“弧度”一词。arc系统在微积分的学习中显示出明显的优越性。例如,这两个重要的“美丽”结论


如果x取角系,就会变成这两个“丑”的公式。


总之,弧系能让我们感受到数学的“简洁之美”。


