中学时,我们都学会了用“度”来描述角的大小,比如圆角360°,直角180°,直角90°,等等。
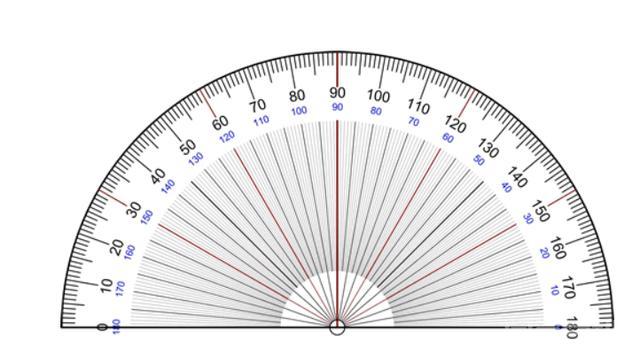
而且高中的时候我们把角度的单位从“度”改成了“弧度”。此时,上述所有角度都已转换如下:
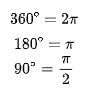
实际上,对于任意角度N,都可以通过下面的公式转换成ι弧度:
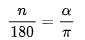
这对于学过高中数学的人来说并不陌生,但学生往往只记住了这种变换方法,却不明白我们为什么要把180度变成无理数,或者可以更直白地问灵魂:初中好像是用角度系统来描述对角线的大小的,那为什么还要引入和学习圆弧系统呢?它的意义是什么?
今天大小吴就和大家探讨一下这个问题。
1.角度系统的起源
这一切都要从角系统和弧系统的历史说起。
在富饶的美索不达米亚平原上,公元前的古巴比伦人主动将圆分成360等分,取其中一等分称之为1“度”,记为1。度数下面有“分”和“秒”的单位,60分为1度,60秒为1分。这是最早的角度系统。

但由于历史悠久,我们无从得知巴比伦人是何时顿悟想出这种测量方法的,也不知道他们为什么要把周长分成360等分。后人主要是这样解释的:
古巴比伦人熟悉60年的计算。
60是一个相对简洁的数字,接近一年中的天数。
30可被8整除,所以圆角为360度时,直角、直角、半直角等典型角度都是整数。
30°有多个因子,使得各种正多边形的内角刚好是整数度(正N边形的内角是[180 (n-2)]/n)。
也许是因为以上原因,聪明的巴比伦人最终选择了360这个神奇的数字作为角度系统的开始。毋庸置疑,它是一个完美的体系,深深影响了后世的数学,并被广泛应用于天文学、航海、测绘等诸多领域,直到现代社会的每一个学生都不得不借鉴。
2.弧度的雏形
巴比伦人对圆的划分在一定程度上影响了后来的古希腊天文学。在古希腊,“地心说”非常流行。人们认为太阳绕着地球做圆周运动,这导致了许多计算圆轨道的问题。此外,人们想知道当弧长已知时,如何找到相应的弦长。正因如此,古希腊希帕科斯(公元前190-120年)第一次绘制了和弦表,托勒密的《大成》一书中也发现了类似的和弦表,使和弦表的思想广为人知。

“地心说”的代表人物托勒密
什么是字符串表?做弦表的目的是在一个半径固定的圆上,求给定圆弧的弦长。Pacos列出了各种弧长L对应的弦长chord(l)(以单位圆为例,弦长已换算成小数):
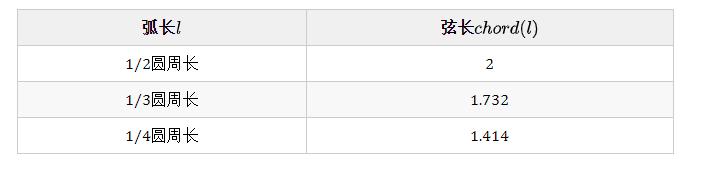
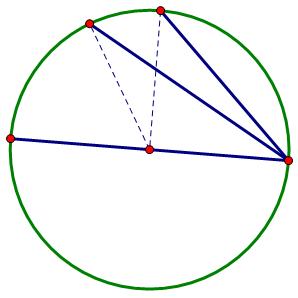
实际弦表中还有很多其他数据,利用这个表可以解决一系列天文问题。
古希腊人还通过弦表找到了弧长与弦长的一一对应关系,这是最早的三角函数。但是,古希腊人并没有形成“功能”的概念。他们不知不觉地把弧长作为三角函数的自变量,为了单位的统一,他们沿袭了巴比伦人的60进制,用60进制表示弧长的度量。
其实这就是弧度的雏形,“弧长与弦长的对应”可以进一步转化为“角度大小与弦长的对应”。由于以弧长为自变量时需要给出圆的半径,所以以弧度(角度大小)为自变量时不需要给出半径,避免了繁琐的换算。这也就不难理解,后人发明和引入弧系是非常自然和必要的。
3.半弦表
公元6世纪,印度数学家aryabhata遵循Hipakos的弦表思想,进一步做出了半弦表。其中他将弦对着的弧的一半对应于弦的一半。看下图。是不是感觉很熟悉?是的,我们知道在单位圆里,这里的半弦是正弦。所以印度数学家发明的半弦表非常接近现代数学中正弦的定义。在随后的数百年间,文明的交流使得半弦琴在阿拉伯、印度、中国等地区广泛流传。同时第一次出现了余弦、正切等三角概念。
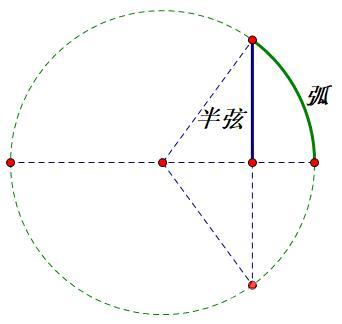
但这一时期的各种三角函数表,仍然是给定半径的(半)弧长与(半)弦长的对应关系,而且形式上大多是表格,角度的范围也只限于[0,180],并没有真正形成抽象的“三角函数”。
4.arc系统的产生和建立
时间来到14世纪,随着欧洲文艺复兴的兴起,数学和三角学再次繁荣起来。
哥白尼的学生、印度数学家利特克斯在研究古希腊数学时发现,给定半径的圆的角度和弧长其实可以一一对应。所以他在改变正弦的定义上取得了突破。在他之前,正弦的定义是:

Ticks将其更改为:


这真是一个巨大的突破!这样一来,三角学中三角比的定义不再依赖于圆,而只能在直角三角形中讨论。正因为如此,角度成为了三角函数的自变量,随后弧系逐渐走上了历史舞台。

几百年过去了,直到那个被苹果砸中的神一样的人的出现,微积分才终于成为数学的主流。进一步,人们开始研究包括三角函数在内的各种抽象函数,人们早已习惯使用十进制,这当然也包括弦长的计算。
但这样会造成一个问题:十进制中的弦长与十六进制中的角度不统一,人们在查阅三角函数表时会感到极其繁琐。在这种情况下,角度系统终于不再适合人们对数学研究的需求。
于是,人们开始考虑用新的单位制来测量角度,弧度制终于诞生了!弧度是由英国数学家罗杰·科尔特斯在大约1714年提出的。这位伟大的数学家深知这种测角方法的优越性和必要性。
5.圆弧系统与数学公式的兼容性
在弧系下,很多微分、积分、级数公式在形式上得到了简化,这也是后来数学家偏爱弧系的原因。
以数学分析中最重要、最基本的极限为例:

这个公式是基于弧系的,所以才这么美观简洁。如果这里的角度x是在角度系统下讨论的,由于角度系统下的数据是圆弧系统下的180/π倍,那么重要的极限就变成了:

这个公式很不雅观。
另一个例子是正弦函数的导数公式:

这种简洁的形式仍然可以出现在arc系统下,它会变成:

你会选择学哪个公式?毫无疑问是前者。
包括最经典的“上帝公式”

它将数学中最重要的常数与最重要的两个实数完美地结合在一起,而这样美丽的形式只有在弧系下才能产生。
现在,你知道我们为什么要学习arc系统吗?
参考文献[1]蒋卓浩,何。电弧系统发展的历史渊源[J].数学通报,2016,55(07):14-17。[2]李忠。为什么要用电弧系统[J]。数学通报,2009,48 (11): 1-3
内容仅代表作者观点。
不,我代表中国科学院物理研究所
来源:大小吴的数学课堂
编辑:趣味超人


