转到网上一个很有意思的问题:

这个问题乍一看似乎很扯淡,但其实是一个很深奥的问题,涉及到抽象代数的一些基本概念,所以打算写一篇文章详细阐述一下。
人类的数学是从计数开始的,最早的概念是自然数。后来随着数学应用范围的扩大,出现了新的数的类型。
初中的时候,我们详细介绍了数制。
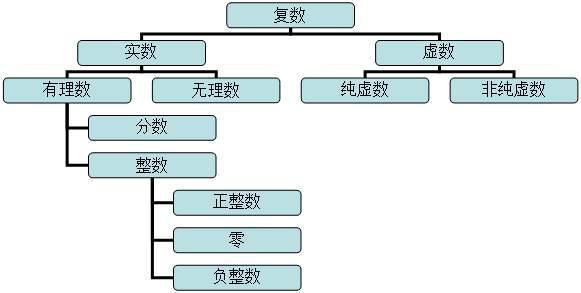
到了高中,我们又学习了集合的概念,从集合的角度学习数。对于叙述方面,我们用一个字母来表示由不同类型的数字组成的集合。我们学到了以下内容:
自然数集:n整数集:z有理数集:q实数集:r复数集:c我相信很多朋友在这里都会遇到和这位网友一样的问题:无理数也是一个很重要的数类型,为什么他们的集合不用字母来表示?是书里忘了提,还是说数学家懒得起名字?
其实无理数集不用字母表示是有原因的。要理解这个道理,首先要理解三个基本概念:集合、二元运算、闭。
基本概念集合集合的概念我们很清楚,它是指由具有某些特定性质的元素构成的集合。当然,关于集合的确切定义还有很多需要讨论的地方,但是理解这个层面就够了。
其实我们对二元运算已经很熟悉了,只是之前没有给它一个精确的定义。用不太正式的语言描述,二元运算就是把两个数变成一个数的对应规律。比如加法是二元运算,因为它把1和1变成2,2和3变成5,等等。同样,加减乘除四则运算都是二元运算。
但是我们一般把减法看成是加法的逆,把除法看成是乘法的逆,所以基本的二元运算只有两种。

所以有人会问,既然有二元运算,那还有一元运算吗?当然有。所谓一元运算,无非是把一个数换成另一个数。我们常见的运算,比如对数运算,平方根运算,都是一元运算。但其实所谓的一元运算,就相当于我们学过的函数。
同样,还会有三进制运算,四进制运算,N进制运算等等,就不多讨论了。

闭包“闭包”其实是理解这篇文章的核心概念。
闭包基于集合和二元运算的概念。
对于某个数集和一个运算,如果从数集中随机选取两个数,二元运算的结果仍然是集合中的数,所以对于二元运算,数集是封闭的。
举个最简单的例子,自然数集对加法是封闭的,因为任意两个自然数相加的结果还是自然数。自然数集不关闭减法。例如,我可以说出两个数字,2和3。都是自然数,但是2-3=-1,所以不是自然数。

要回答本文中提出的问题,我们必须从闭包的概念开始。
我们先分析一下已知集合对四则运算的封闭性。
自然数集对于加法和乘法是封闭的,对于减法和除法是不封闭的。整数Z对于加减乘除是闭的,对于除法不是闭的。有理数集Q对于所有四种运算都是封闭的。实数集R对于四则运算是封闭的。复杂集C对于所有四个操作都是封闭的。在这里,我要特别强调有理数集。有理数集对加减乘除四则运算的封闭不是一件显而易见的事情。我们需要有严格的证据。
有理数是可以写成两个整数之比的数,那么我们假设有两个有理数b1/a1和b2/a2,其中a1、b1、a2和b2都是整数。让我们来看看他们四个操作的结果:

可以看出,四则运算的结果仍然是有理数,证明了有理数集对四则运算是封闭的。
这里我想说的是,数学家证明了有理数集是接近加减乘除四则运算的最小数集。也就是说,任何比有理数小的集合,哪怕只比有理数集合小一个数,也不再对加减乘除四则运算封闭。

在抽象代数中,我们把接近加减乘除四则运算的集合称为数域。可以看出,实数集和复数集都是数域。我们上面提到的结论是有理数集是最小数域。换句话说,任何数域都包含一组有理数作为它的子集。
分析完无理数集,我们再来看无理数集。我们会发现无理数和四则运算都不是闭的。我们可以很容易地举出例子:
对,加法:√2和-√2是无理数,但是加在一起等于0,0不是无理数。减法的例子:√2和-√2可以看成√2-√2,结果也是0。乘法:√2×√2,结果是2,2不是无理数。对于除法:√ 2悚2,结果是1,1不是无理数。

原来无理数集合就是这么烂的集合!这就是为什么我们不给它一封信。
在近代代数中,数学家主要关心的是集合以及集合中元素的运算结构,由此产生了群、环、域等一系列概念。
集合上的一个运算是闭的,所以研究它是有意义的,会有很多奇妙的性质。但如果操作不封闭,研究就会混乱,没有意义。

对于前五个集合,至少有一个运算使它们闭合,所以我们可以利用这个闭合来获得许多新的性质,解决许多数学问题,甚至构造更复杂的组合。数学家经常使用这五个集合。为了叙述方便,他们取五个字母代替。
但对于无理数集,由于它不是对四则运算封闭的,所以它不能得到前五个集合那样丰富的性质,也没有它们那样被频繁使用,所以我们不需要用单个字母来命名。
说到这里,不得不提一下近世代数的发展。
群是近代代数中最重要的概念,起源于19世纪法国数学天才伽罗瓦(1811 ~ 1832)。高尔瓦利用群论的方法,彻底解决了五次或五次以上方程的根式解问题,这是数学发展史上划时代的事件。我这位前所未有的数学天才在21岁时因为一场意外而英年早逝,这是人类数学史上的一大遗憾。

然而,我们现在在教科书上所学的代数之所以是这个样子,主要是因为20世纪德国女数学家艾米·诺特(1882 ~ 1935),她被誉为“现代代数之母”。诺特是数学史上无可争议的最伟大的女数学家。他和他的学生组成的诺特学派完全改变了代数的全貌。



