一道初中几何题——求正方形中等边三角形的面积
在ABCD正方形中有一个等边三角形CMN。如果正方形的边长是1,求等边三角形的面积。
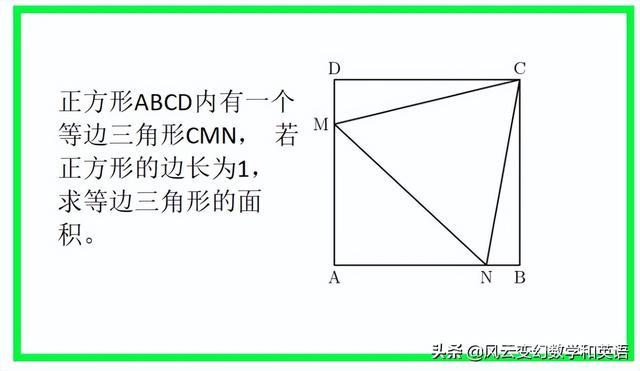
解法:由于CMN是一个等边三角形,CM=CN=MN,另一个正方形CD=CB,则直角三角形CDM和直角三角形CBN全等,所以得出NB=MD,设NB=x,根据勾股定理:
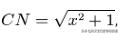
另外,AN=AM=1-x,
对于等腰直角三角形:
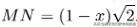
根据等边三角形CM=MN:
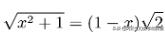
解这个方程:
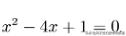
由此,找出:
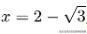
另一个根被截断,因为它大于1。
因此:
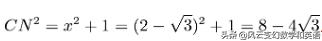
这里不需要直接求解CN,因为需要三角形的面积。
在等边三角形中,如果边长是x,那么它的面积是:
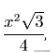
这个公式用等边三角形的高为(√3x)/2,底为x,很容易证明。对于准备考试的初中生来说,应该是理解和记忆,或者直接现场推导。
将上面CN的平方带入这个公式:
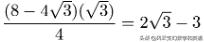
这是等边三角形CMN的面积。
根据上面的推导,可以知道过正方形顶点的等边三角形只有一个。