虽然近代中国对世界数学发展的贡献有限,但如果时光倒流一千百年,古代中国的数学成就绝对会屹立不倒。
《九章算术》是中国数学发展的历史记录。这本书继承了以往所有的数学成果,将多种类型的问题进行分类,形成一套非常实用的实际问题。对于球的体积计算公式,这里也提到一个。
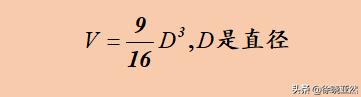
《九章算术》中球体体积的计算公式
你没有看错。作为计算球体体积的公式,这个公式里没有π,因为这个公式是古人通过实测得到的!现在看来确实很荒谬,但当时人的数学能力确实有限,即使有怀疑也只是直觉,很难提出确凿的证据,更别说修正这个公式了。

刘辉
魏晋时期,中国诞生了一位非常伟大的数学家刘徽。如果不算20世纪,那么刘徽绝对是中国历史上最有成就的数学家。他的研究非常广泛,几乎涉及中国古代数学的所有领域。他建立了分数和方程理论,对割圆进行了深入研究。他第一个得到了更精确的π值。刘徽的两部著作流传于世,对后世影响很大,几乎成为一千多年来学习算术的官方教材。这是九章算术笔记和岛屿计算。在《九章算术注》中,刘徽正式质疑了上述计算公式。
在这里,刘辉构造了一个特殊的结构,“牟和方盖”。
两个底径相同的圆柱体正交,公共部分剥离。这是牟河方盖。

斯坦梅茨固体
这个立体构造好之后,我们发现,如果用一组平行于地面的平面来切割这个立体,横截面都是正方形,而这个正方形正好在与球体相同的高度上外切横截面。这段话有点抽象,用下图来表示。(这张图真的不好画,所以直接在网上找的。)
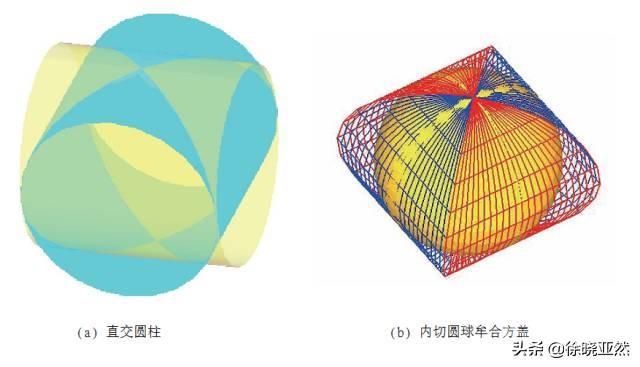
刘辉其实这个时候就知道内切圆和外接圆的面积是4: π。换句话说,这个牟河方盖的体积与内接球体的体积之比也是4: π。如果刘辉能算出牟和方盖的体积,那么球的公式就一定能得到。而刘辉却走不下去了,因为牟和方盖的构造方法虽然很简单,只够让两个等宽的圆柱体正交,但很难要求这种共同的部分,至少在当时已经有了数学理论。刘辉虽然没有踏入最后一步,但是他提出的牟河方盖结构是极其正确的,这个方向没有问题。通过粗略估算这个牟和方盖的体积,刘辉也完全否定了原来《九章算术》中计算球体积的公式。

祖冲之

祖轩
接下来,必须有人计算出正确的公式,这需要一种新的方法来工作。于是两三百年后,故事发生在了祖家。老爹祖冲之当然有名,应该算是有名的计算大师。圆周率小数点后七位的成绩不是盖的。这里说的是他的儿子,祖宣。父子都是数学家,祖宣最著名的贡献是祖鲁原理。在这里,提取原则的精髓:
“如果命运和力量相同,产品就不可能不同。”
古人真的惜字如金,翻译过来就是:如果两个物体的截面积和高度永远相等,那么体积也是一样的。
上图很清楚。

很明显,左边是一摞垂直摆放的书,右边是逐渐倾斜的。我们可以想象一下,把这一摞平行面的书切开的时候,每次的横截面都是书页的大小。很明显,横截面积总是相等的,当然高度也是相等的。因为只是一摞书的两种状态,体积当然是相等的。那我们再举一个一般的例子。左右两边是完全不同的对象,但也符合祖鲁原则的要求。这时候成交量就不一定那么好对比了。
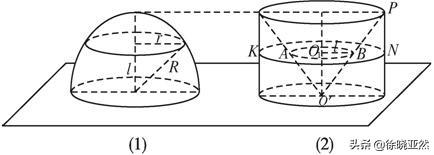
祖父子构造的两个等体积物体
先提出祖冲之父子的推导过程。

球形体积的公式是根据祖鲁原理推导出来的。
结果祖父子终于得到了正确的球体积公式,终于弥补了刘辉的未竟事业。
这是中国古代数学中极限思想的又一次开创性体现。尽管祖父子在他们的著作中根本没有提到极限这个词,但这个原理背后的微积分雏形是相当明显的。如果用现在微积分的思想来考虑,祖鲁的原理其实是下面这个公式:
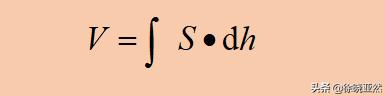
祖鲁原理的微积分表述
截面积已知的情况下,我们逐步求出高度的微分。如果能得到解析公式,就可以通过直接积分得到公式。如果高度的差异化不容易获得,我们也可以通过细分来寻找差异化,最后结合在一起寻找整合。
利用祖鲁原理可以计算一些复杂物体的体积。解决的关键在于如何构造一个已知体积的物体,使其与待计算的物体具有相同的横截面和高度。我相信祖父子是经过了无数次的实验,才最终构造出半球和挖圆柱体的例子。
当然,有很多方法可以得到球体积的公式,甚至任何规则曲线绕其轴旋转形成的物体的体积都可以很容易地计算出来:
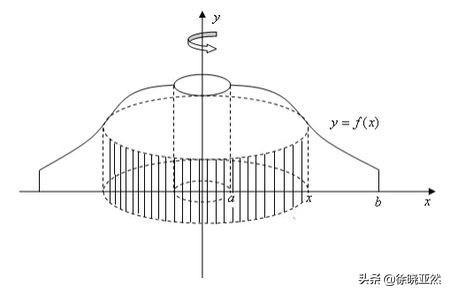
通过绕轴旋转曲线形成的物体。
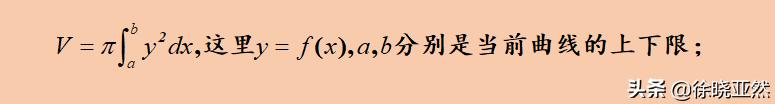
曲线绕轴旋转得到的体积公式
如果要计算球的体积公式,可以直接把圆的方程曲线代入上面的公式得到结果。
祖先树的原理也领先世界很多年。直到17世纪,意大利数学家卡瓦列里才提出了类似的成果,比祖冲之父子晚了1100多年。
父亲计算圆周率,儿子计算球的体积。反正数学家父子真的和圈子有很大的缘分。我又想起了欧拉和他的老师伯努利的故事。在学术研究中,没有什么比父子传承和师徒传承更好的了。


