我一直觉得数学物理中的各种常数是最牛逼的东西。他们似乎是自宇宙诞生以来就被上帝精心挑选的。那一串无穷的数字常常让人陷入沉思的无底洞——为什么这一串数字就这样呢?下面是作者举的几个例子,希望你有所收获。
素数的特殊形式
费马数()
费马数是以数学家费马命名的一组自然数,其形式为:
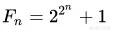
其中n是一个非负整数。
如果2^n+1是一个质数,我们可以得出n必须是2的幂。所有形式为2^n+1的素数必定是费马数,这些素数称为费马素数。只有五个已知的费马素数F0到F4。
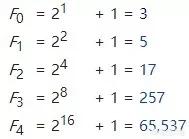
1640年,费马提出了一个猜想,即所有费马数都是素数。这个猜想适用于最小的五个费马数,所以费马声称他已经找到了素数的公式。但是,欧拉在1732年否定了这个猜想,他给出了分解公式:
F5 = 2^32 + 1 = 4294967297
= 641 × 6700417
费马之后的欧拉,虽然推翻了“费马数”的结论(“费马数”是素数的普遍公式),证明了费马小定理的正确性,并使用了《代数指南》中的“无限下降法”,使之成为数论研究中的重要方法和技巧之一,但仍未能统一许多理论,使初等数论成为一个完整的理论体系。

欧洲17世纪数学网络枢纽,马兰·梅森,梅森数
2 p-1形式的一类数,其中指数p是素数,通常称为Mp。如果梅森数是一个素数,则称为梅森素数。早在公元前300年,古希腊数学家欧几里德就开创了2 P-1的研究。他在其名著《几何原本》第九章讨论完全数时指出,如果2 p-1是素数,那么2 p-1 (2p-1)就是完全数。
前几个较小的梅森数多为素数,但梅森数越大,梅森素数越难出现。
2019年,据国外媒体报道,据梅森素数(Mersenne Prime)的梅森素数搜索(GIMPS)项目官方消息,一名来自美国佛罗里达州的35岁IT专业人士发现了人类已知的最大的梅森素数。这个素数叫做M82589933,是已知的第51个梅森素数2 82589933-1(即2的82589933次方减1)。
质数是指在大于1的整数中,只能被1和它本身整除的数。素数有无穷多个,但目前只有极少数的素数可以表示为2 p-1 (p是素数),这就是梅森素数(如3,7,31,127等。).它是以17世纪法国数学家马林·梅森的名字命名的。
梅森素数在当代具有重要的理论意义和实用价值。这是寻找已知最大素数的最有效方法;它的探索促进了数论这一数学女王的研究,促进了计算技术、编程技术、密码学技术和快速傅立叶变换应用的发展。
探索梅森素数的最新意义在于它促进了网格技术的发展。网格技术将是一项应用非常广泛、前景诱人的技术。另外,搜索梅森素数的方法也可以用来检验计算机硬件操作是否正确。
由于梅森素数的探索需要多学科多技术的支撑,许多科学家认为梅森素数的研究成果在一定程度上反映了一个国家的科技水平。英国顶级科学家M.Sautoy甚至认为这是科学发展的里程碑。相信梅森素数这颗数学海洋中的璀璨明珠,正以其独特的魅力吸引着更多有志之士去探索和研究。
数学中有特殊意义的常数钦钦常数K ≈ 2.685452
每一个实数都可以写成a0+1/(a1+1/(a2+…))的形式,其中a0,a1,a2,…都是整数。我们把[A0;A1,a2,a3,…]称为这个数的连分式展开式。与小数展开相比,连分式展开更加优雅美观,这使得连分式成为数学研究的必修课。
在1964年出版的一本连分数的数学教材中,数学家钦钦证明了这样一个惊人的结论:除了有理数和二次整系数方程的根等一些特例,几乎所有实数的连分数展开式序列的几何平均值都收敛于同一个数,大约为2.685452。比如圆周率的连分式展开数列,前20个数的几何平均值约为2.62819,前100个数的几何平均值约为2.69405,前100万个数的几何平均值约为2.68447。
目前,人们对这个神秘的常数了解不多。虽然钦钦常数很可能是无理数,但至今未被证明。而钦钦的确切数值并不容易得到。1997年,David Bailey等人优化了一个收敛速度极快的数列,但只找到了钦钦的7350位小数。
康威常数λ ≈ 1.303577269
你能找出下列数列的规律吗?
1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, …
这个数列的规律简单有趣。序列中的第一个数字是1。从第二个数字开始,每个数字都是对前一个数字的描述:第二个数字11表示其前一个数字是“1 1”,第三个数字21表示其前一个数字是“2 1”,第四个数字1211表示其前一个数字是“12,1 1 1”……这个有趣的序列被称为“出现序列”。
外观系列有很多有趣的属性。比如,虽然数列中的数字会越来越长,但数字4永远不会出现。1987年,英国数学家约翰·康威发现,在这个数列中,两个相邻数的长度之比越来越接近一个固定的数。最终,数列长度的增长率将稳定在一个常数1.303577左右。约翰·康威将这个常数命名为康威常数,并用希腊字母λ表示。约翰·康威证明了λ是一个无理数,并且它是一个71次方程的唯一实数解。
尚珀诺常数C10 ≈ 0.1234567
把所有正整数从小到大排成一行,前面加一个小数点,得到一个无限小数...20000.000000000005这个数字是英国统计学家尚珀诺内于1933年构建的。他把它命名为Champernowne常数,用符号C10表示。与其他数学常数相比,Champernowne常数有一个很大的区别:这个数只是人为定义来论证某些数学问题的,它并不描述任何数学对象。
Champernowne常数有许多有价值的性质。首先,很容易看出它是一个无限无环小数,所以它也是一个无理数。其次,它也是一个“超越数”,也就是说它不是任何整系数多项式方程的解。也是一个“正态数”,意思是每个数字或数字组合出现的机会都是均等的。在许多数学领域,尚珀诺韦常数显示出其非凡的意义。

物理中的一些特殊数字,不懂基本意思,基本可以告别物理考试了!
物理学中有一些特殊的数,有些是常数(常量),有些是定量的基本单位。
0摄氏度(℃)或0开尔文(K)0摄氏度(℃)是摄氏温标的零度,0开尔文(K)是热力学温标的零度,即绝对零度。
两者之间的关系是:
0℃= 273.15k;
0K=-273.15℃
绝对零度(0K)是低温的极限,理论上达不到。
1大气压= 760毫米汞柱= 76厘米汞柱= 1.013×10 ^ 5帕= 10.336米H2O。
随着科学技术的发展,标准大气压值发生了几次变化。最初规定海平面上的大气压是温度为0℃,纬度为45°时的标准大气压,其值约为76 cm Hg。后来发现,在这种条件下,大气压力是不稳定的,它在风和温度的影响下发生变化。因此,76厘米汞柱的高度被定义为标准大气压值。但是后来发现76 cm Hg的压强值也是不稳定的,水银的密度会随着温度的影响而变化。g的值也随纬度而变化。为了保证标准大气压是一个恒定值,1954年第十届国际计量大会的决议规定,标准大气压值为:
1标准大气压= =101325 N/m^2.
1原子质量单位1u = 1.660566× 10-27kg。质子的质量是1.007277u,中子的质量是1.008665u,氦核(α粒子)的质量是4.001509u根据爱因斯坦质能方程E = c2m(δE = C2δm),发生核反应时,如果反应前后的质量损失1个原子质量单位,则释放的能量为。
E=(3×108)2×1.660566×10‾27
= 1.4945094× 1010焦耳
=931.5兆电子伏
在天文研究中,宇宙的大小和星系之间的距离都很遥远,以光年为计量单位更为合适。
1T相当于同量地球的倍数,可以方便形象地将地球与其他星球进行比较。电子1EV = 1.6× 10-19J,即电子在电场中被1 V的加速电压加速后的动能。电子伏特的值通常表示电场中带电粒子的能量。

光速c = 3×10 ^ 8m/s,人们常说光速是30万km/s,但实际上,光在1 s内行进的距离是299,792,458m,即299792458km/s,光速是目前已知的最大速度。当一个物体达到光速时,它的动能是无限的,所以按照目前人类的认知是不可能达到光速的。
ππ= 3.14。π应该是数学的“专属”数,但在物理学的研究中,尤其是在曲线运动的研究中却经常用到。
热量的机械当量j = 4.18j = 1卡。随着测量热量的单位卡(千卡)被废除,旧教材中出现了热量的机械当量。热量的机械当量反映了热量与能量的相当关系,即1卡的热量相当于4.18 J的能量。19世纪40年代,英国物理学家焦耳设计了测量用的实验装置,用不同的材料反复实验,不断改进实验设计,最终测得了更精确的当量值。
重力常数g = 6.67×10-11n·m2/kg 2。这个常数与万有引力定律有关。万有引力定律是牛顿提出的,它的表达式是:F = GMM/R 2。引力常数是由英国物理学家卡文迪许设计的扭秤测量的。他的实测值为6.754×10-11n·m ^ 2/kg ^ 2,与后来的公认值仅相差1.26%。该值的测量意义重大。
普朗克常数h = 6.6260693×10^-34 j s s . 1900年,德国物理学家普朗克在研究电磁辐射的能量分布时发现,只有当他认为电磁波的发射和接收不是连续的,而是一个接一个的,各部分的能量等于hν时,理论计算的结果才能与实验事实完全一致,其中ν是光的频率,h是一个普适常数,称为普朗克常数。普朗克建立了量子力学的新理论。受此理论启发,为了解释光电效应定律,爱因斯坦于1905年提出空之间传播的光不是连续的,而是一个接一个的。每一个称为一个光子,光子的能量与其频率成正比,即E = hν,其中H是普朗克提出的普朗克常数。这个理论后来被称为光子理论。
单位制有7个基本单位。在单位制中代表长度的米(m );千克(kg)的重量;代表时间的秒;开尔文(k)代表温度;摩尔(mol)代表物质的量;安培(a)来表征电流强度;光强的坎德拉(kd)。
76 cm Hg 76 cm Hg是一个标准大气压值,也就是说76 cm Hg产生的压力是1个标准大气压。
静电力常数为9.0×10-9n·m2/C2。用库仑扭秤装置得出著名的库仑定律F = kQ1Q2/r^2,并测得静电力常数。
931.5 MeV,这就涉及到爱因斯坦的质能方程,即E = C 2m(δE = C 2δm)。当核反应发生时,如果反应前后的质量亏损为1原子质量单位,将释放出931.5 MeV的能量。
地球表面的重力加速度实际上是9.8 m/s^2(平均),为计算方便,常取10 m/s^2。初中没有引入重力加速度概念的时候,是用常数G来反映重量和质量的关系。G=mg,g = 9.8 N/kg,即质量为1 kg的物体在地球表面附近的重量为9.8 N。

