我查了一些新闻资料。2000年以前,我们的小学课本上几乎都说0不是自然数,最小的自然数是1。
所谓“自然数”,就是人类最初计数时使用的数。东西是一个一个数的,所以是1,2,3……至于0,不管是罗马,希腊,埃及,巴比伦,甚至是汉字,数的时候本来就没有0,因为没有的时候说“没有”就好。人们不认为它是一个数字。

后来印度人发明了完整的十进制计数法,可以写出10、100这样的数字。这些数字中虽然有零,但只是作为“占位符”使用。换句话说,人们仍然不认为一个零有任何意义。
后来,直到公元600多年,印度数学家布拉马普特拉·古普塔才真正提出0的概念。但是,他之所以需要0,很大程度上是因为他需要将数扩展为负数。一旦扩展到负数,他就得指定一个0作为正数和负数的分界点。
所以,一直以来,数学家们普遍认为0的必要性伴随着负数而来。如果只是数数,不研究负数,根本不需要0。所以最简单的“自然数”应该不包括0——我们这一代人小时候也学过这个,也就是说最小的自然数是1。

事实上,自然数是由一套叫做阿砣算法的规则定义的。钢琴算术使用几个公理来定义自然数。
然而,现在情况不同了。2000年左右,全国范围内出现了一次教科书的改版,大部分版本的教科书都把0算作自然数,一直沿用至今。比如人教版四年级数学第一册是这样写的:

其实很长一段时间,0是不是自然数的问题是有争议的。一种观点认为,0作为数字使用时,出现负数的时间,比正整数晚很多,所以0应该符合负整数,而自然数应该只有正整数。
另一种观点认为,本质上0和正整数更相似,在很多领域(如集合论、逻辑学、计算机科学)把0和正整数放在一起更方便。例如,集合中的0表示空集合。一个集合可以是空(有0个元素),也可以有1,2,3 …个元素,但不能有负元素;在计算机中,0和正整数的表示方式相同,而负整数需要补码。

事实上,世界上对自然数有不同的定义。以法国为代表的大多数国家认为自然数是从0开始的。我们的教材一直沿用前苏联的说法,0不是自然数。为了方便国际交流,中国还在1993年制定了一个新标准,将0包括在自然数的集合中。2000年,教育部主持教科书改编会议时,明确提出将0归为自然数。这次修改也符合国际惯例。
这样一直打下去是没问题的,尤其是随着全球化的发展,一切都得有个标准,这是国际标准化组织(ISO)的工作。1992年,ISO发布了国际标准ISO 31:1992,明确定义了数学符号和符号的书写和含义。
在本标准中,自然数n的定义是“自然数集、自然数集、正整数集和零”,并在注释中给出了一个例子:
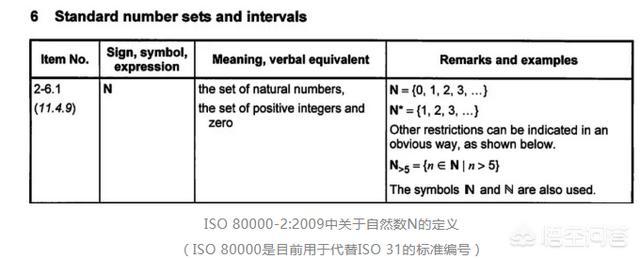
现在国际标准出来了,我们国家标准也得跟上。于是,1993年,我们发布了国家标准GB 3102:93,至今仍是强制性标准。上面写着:

既然国家标准都出来了,我们的小学教材和国家标准不一样,似乎有点说不过去,于是就用国家标准把教材改成了现在的样子。
在传统的自然数集合中加入“0”,仍然保持所有的“运算规则”。比如新自然数集合{0,1,2,…,n,…}中任意两个自然数可以相加相乘,运算结果仍然是自然数。同时,加法和乘法的结合律和交换律,乘法的分配律也不会受到影响。
所以“0”加入自然数集是很自然的,而不仅仅是人为的“规定”。它帮助我们更好地理解自然数及其作用,同时使我们认识到,我们不仅要知道和记住数学的定义和规律,还要思考规律背后的数学意义。
所以一定要记住,现在小学课本上0是自然数。如果考试问你“最小的自然数是多少?”记得回答0而不是1。

虽然ISO和GB中有明确的规定,但并不是所有人都熟悉这些标准,所以为了避免歧义,我们干脆不用“自然数”这个词了。为什么我们要纠结这个词?
如果不想包含0,就说“正整数”。如果要包含0,就说“非负整数”。这个最清楚了吧?
